Menguasai Matematika Kelas 7 Semester 2: Panduan Lengkap dengan Contoh Soal dan Pembahasan
Semester 2 di kelas 7 SMP merupakan fase penting dalam perjalanan belajar matematika siswa. Materi yang diajarkan cenderung lebih kompleks dan membutuhkan pemahaman konsep yang lebih mendalam dibandingkan semester sebelumnya. Topik-topik seperti aljabar, persamaan linear, bangun datar, dan statistika mulai diperkenalkan, yang menjadi fondasi penting untuk materi matematika di jenjang selanjutnya.
Memahami dan menguasai materi matematika kelas 7 semester 2 bukan hanya sekadar memenuhi tuntutan kurikulum, tetapi juga membekali siswa dengan kemampuan berpikir logis, analitis, dan pemecahan masalah yang sangat berguna di berbagai aspek kehidupan. Oleh karena itu, latihan soal yang terstruktur dan terarah menjadi kunci keberhasilan.
Artikel ini hadir untuk membantu siswa kelas 7 dalam mempersiapkan diri menghadapi ujian atau sekadar memperdalam pemahaman materi matematika semester 2. Kami akan menyajikan berbagai contoh soal yang mencakup topik-topik utama, lengkap dengan pembahasan mendalam dan langkah-langkah penyelesaiannya.

Topik Utama Matematika Kelas 7 Semester 2
Sebelum kita melangkah ke contoh soal, mari kita tinjau kembali topik-topik utama yang biasanya dipelajari di kelas 7 semester 2:
-
Aljabar:
- Bentuk Aljabar: Pengertian variabel, konstanta, suku, suku sejenis, suku tak sejenis.
- Operasi pada Bentuk Aljabar: Penjumlahan, pengurangan, perkalian, dan pembagian bentuk aljabar.
- Persamaan Linear Satu Variabel (PLSV): Pengertian, cara menyelesaikan PLSV.
- Pertidaksamaan Linear Satu Variabel (PtLSV): Pengertian, cara menyelesaikan PtLSV.
-
Bangun Datar:
- Keliling dan Luas Persegi Panjang, Persegi, Jajar Genjang, Trapesium, Layang-layang, Belah Ketupat, Segitiga, dan Lingkaran.
- Hubungan antara Keliling, Luas, dan Sifat-sifat bangun datar.
-
Statistika:
- Pengumpulan dan Penyajian Data: Tabel, diagram batang, diagram garis, diagram lingkaran.
- Ukuran Pemusatan Data: Mean (rata-rata), Median (nilai tengah), Modus (nilai yang paling sering muncul).
Mari kita mulai dengan contoh soal dan pembahasannya.
>
Contoh Soal dan Pembahasan Matematika Kelas 7 Semester 2
Bagian 1: Aljabar
Soal 1: Menyederhanakan Bentuk Aljabar
Sederhanakan bentuk aljabar berikut: $5x + 3y – 2x + 7y – 10$
Pembahasan:
Untuk menyederhanakan bentuk aljabar, kita perlu mengelompokkan suku-suku sejenis. Suku sejenis adalah suku-suku yang memiliki variabel yang sama dengan pangkat yang sama.
- Suku yang mengandung variabel $x$: $5x$ dan $-2x$
- Suku yang mengandung variabel $y$: $3y$ dan $7y$
- Suku konstanta (tidak memiliki variabel): $-10$
Sekarang, kita jumlahkan atau kurangkan koefisien dari suku-suku sejenis:
$(5x – 2x) + (3y + 7y) – 10$
$= 3x + 10y – 10$
Jadi, bentuk aljabar yang disederhanakan adalah $3x + 10y – 10$.
Soal 2: Mengalikan Bentuk Aljabar
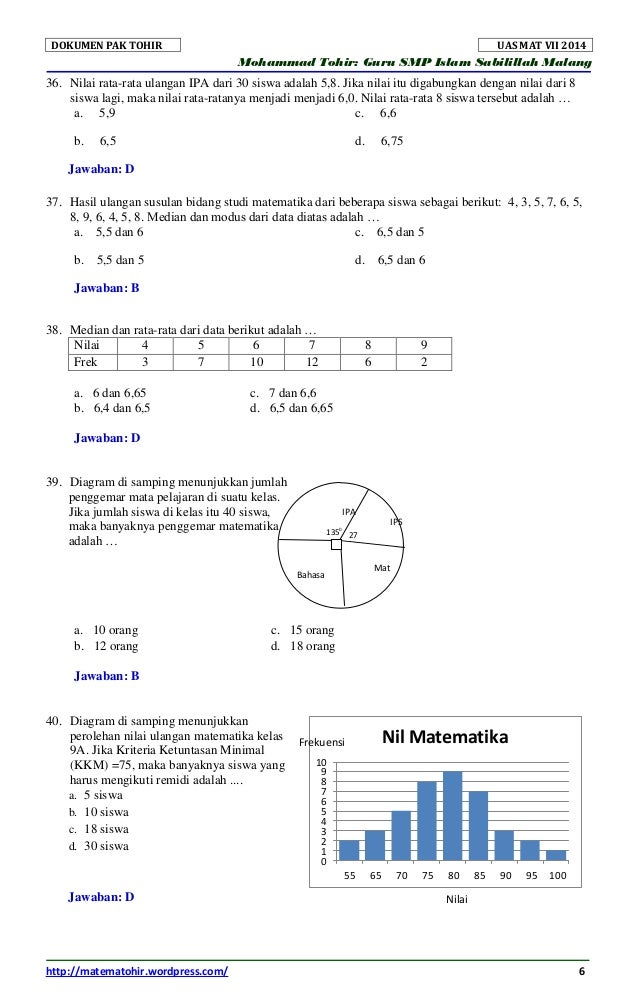
Tentukan hasil perkalian dari $(2a + 3)(a – 4)$
Pembahasan:
Kita dapat menggunakan metode distribusi (pelangi) untuk mengalikan dua bentuk aljabar binomial. Setiap suku di binomial pertama dikalikan dengan setiap suku di binomial kedua.
$(2a + 3)(a – 4) = 2a(a – 4) + 3(a – 4)$
$= (2a times a) + (2a times -4) + (3 times a) + (3 times -4)$
$= 2a^2 – 8a + 3a – 12$
Selanjutnya, kita sederhanakan dengan menjumlahkan suku-suku sejenis:
$2a^2 + (-8a + 3a) – 12$
$= 2a^2 – 5a – 12$
Jadi, hasil perkaliannya adalah $2a^2 – 5a – 12$.
Soal 3: Menyelesaikan Persamaan Linear Satu Variabel (PLSV)
Tentukan nilai $p$ dari persamaan berikut: $4p – 7 = 13$
Pembahasan:
Tujuan kita adalah mengisolasi variabel $p$ di satu sisi persamaan.
Langkah 1: Tambahkan 7 ke kedua sisi persamaan untuk menghilangkan $-7$ di sisi kiri.
$4p – 7 + 7 = 13 + 7$
$4p = 20$
Langkah 2: Bagi kedua sisi persamaan dengan 4 untuk mendapatkan nilai $p$.
$frac4p4 = frac204$
$p = 5$
Jadi, nilai $p$ adalah 5.
Soal 4: Menyelesaikan Pertidaksamaan Linear Satu Variabel (PtLSV)
Tentukan himpunan penyelesaian dari pertidaksamaan $3x + 5 > 14$, jika $x$ adalah bilangan bulat positif.
Pembahasan:
Kita akan menyelesaikan pertidaksamaan ini seperti menyelesaikan persamaan linear, namun perlu diingat bahwa tanda pertidaksamaan akan berubah arah jika kita mengalikan atau membagi kedua sisi dengan bilangan negatif.
Langkah 1: Kurangi kedua sisi dengan 5.
$3x + 5 – 5 > 14 – 5$
$3x > 9$
Langkah 2: Bagi kedua sisi dengan 3.
$frac3x3 > frac93$
$x > 3$
Karena $x$ adalah bilangan bulat positif dan $x$ harus lebih besar dari 3, maka himpunan penyelesaiannya adalah bilangan bulat positif yang lebih besar dari 3.
Himpunan penyelesaian = $4, 5, 6, 7, dots$
>
Bagian 2: Bangun Datar
Soal 5: Luas Persegi Panjang
Sebuah persegi panjang memiliki panjang 15 cm dan lebar 8 cm. Hitunglah luas persegi panjang tersebut.
Pembahasan:
Rumus luas persegi panjang adalah:
Luas = Panjang × Lebar
Diketahui:
Panjang ($p$) = 15 cm
Lebar ($l$) = 8 cm
Luas = $15 text cm times 8 text cm$
Luas = $120 text cm^2$
Jadi, luas persegi panjang tersebut adalah $120 text cm^2$.
Soal 6: Keliling Lingkaran
Sebuah lingkaran memiliki jari-jari 7 cm. Hitunglah keliling lingkaran tersebut. (Gunakan $pi approx frac227$)
Pembahasan:
Rumus keliling lingkaran adalah:
Keliling = $2 times pi times r$ (di mana $r$ adalah jari-jari)
Diketahui:
Jari-jari ($r$) = 7 cm
$pi approx frac227$
Keliling = $2 times frac227 times 7 text cm$
Kita bisa mencoret angka 7 di penyebut dan pembilang:
Keliling = $2 times 22 text cm$
Keliling = $44 text cm$
Jadi, keliling lingkaran tersebut adalah 44 cm.
Soal 7: Luas Segitiga dengan Alas dan Tinggi
Sebuah segitiga memiliki alas sepanjang 12 cm dan tingginya 9 cm. Berapakah luas segitiga tersebut?
Pembahasan:
Rumus luas segitiga adalah:
Luas = $frac12 times textalas times texttinggi$
Diketahui:
Alas ($a$) = 12 cm
Tinggi ($t$) = 9 cm
Luas = $frac12 times 12 text cm times 9 text cm$
Luas = $6 text cm times 9 text cm$
Luas = $54 text cm^2$
Jadi, luas segitiga tersebut adalah $54 text cm^2$.
Soal 8: Menghitung Luas Trapesium
Sebuah trapesium memiliki panjang sisi sejajar 10 cm dan 16 cm. Jika tinggi trapesium tersebut adalah 8 cm, hitunglah luasnya.
Pembahasan:
Rumus luas trapesium adalah:
Luas = $frac12 times (textjumlah sisi sejajar) times texttinggi$
Diketahui:
Sisi sejajar 1 ($a$) = 10 cm
Sisi sejajar 2 ($b$) = 16 cm
Tinggi ($t$) = 8 cm
Luas = $frac12 times (10 text cm + 16 text cm) times 8 text cm$
Luas = $frac12 times (26 text cm) times 8 text cm$
Luas = $13 text cm times 8 text cm$
Luas = $104 text cm^2$
Jadi, luas trapesium tersebut adalah $104 text cm^2$.
>
Bagian 3: Statistika
Soal 9: Menghitung Mean (Rata-rata)
Diberikan data nilai ulangan matematika 5 siswa sebagai berikut: 7, 8, 6, 9, 5. Hitunglah nilai rata-rata (mean) dari data tersebut.
Pembahasan:
Rumus mean adalah jumlah seluruh data dibagi dengan banyaknya data.
Jumlah seluruh data = $7 + 8 + 6 + 9 + 5 = 35$
Banyaknya data = 5
Mean = $fractextJumlah seluruh datatextBanyaknya data$
Mean = $frac355$
Mean = 7
Jadi, nilai rata-rata ulangan matematika siswa tersebut adalah 7.
Soal 10: Menentukan Median (Nilai Tengah)
Diberikan data tinggi badan 7 siswa dalam cm: 155, 160, 158, 162, 155, 165, 159. Tentukan nilai median dari data tersebut.
Pembahasan:
Untuk menentukan median, pertama-tama kita harus mengurutkan data dari yang terkecil hingga terbesar.
Data yang diurutkan: 155, 155, 158, 159, 160, 162, 165.
Jumlah data adalah 7 (ganjil). Median adalah nilai yang berada tepat di tengah setelah data diurutkan. Dalam kasus ini, nilai tengah adalah data ke-($frac7+12$) = data ke-4.
Data ke-4 adalah 159.
Jadi, median tinggi badan siswa tersebut adalah 159 cm.
Soal 11: Menentukan Modus (Nilai yang Paling Sering Muncul)
Perhatikan data frekuensi penjualan buku di sebuah toko selama seminggu:
- Buku Cerita: 25 eksemplar
- Buku Pelajaran: 30 eksemplar
- Buku Komik: 40 eksemplar
- Buku Ensiklopedi: 20 eksemplar
- Buku Novel: 30 eksemplar
Tentukan modus dari data penjualan buku tersebut.
Pembahasan:
Modus adalah nilai atau data yang paling sering muncul atau memiliki frekuensi tertinggi.
Dalam data di atas, kita dapat melihat frekuensi penjualan setiap jenis buku:
- Buku Cerita: 25
- Buku Pelajaran: 30
- Buku Komik: 40
- Buku Ensiklopedi: 20
- Buku Novel: 30
Nilai frekuensi tertinggi adalah 40, yang merupakan frekuensi dari Buku Komik. Namun, jika ada beberapa data yang memiliki frekuensi tertinggi yang sama, maka semuanya menjadi modus. Di sini, frekuensi 30 muncul dua kali (Buku Pelajaran dan Buku Novel).
Frekuensi tertinggi adalah 40 (Buku Komik).
Frekuensi kedua tertinggi adalah 30 (Buku Pelajaran dan Buku Novel).
Modus adalah nilai yang memiliki frekuensi paling tinggi. Dalam kasus ini, frekuensi tertinggi adalah 40, yang dimiliki oleh Buku Komik. Namun, ada juga frekuensi 30 yang muncul dua kali.
Dalam soal ini, jika pertanyaannya adalah "jenis buku yang paling laris", maka jawabannya adalah Buku Komik. Jika pertanyaannya adalah "modus dari frekuensi penjualan", maka kita harus melihat frekuensi yang paling sering muncul.
Mari kita klarifikasi: Modus merujuk pada nilai datanya, bukan frekuensinya. Jadi, kita mencari jenis buku yang frekuensi penjualannya paling tinggi.
Frekuensi tertinggi adalah 40, yang dicapai oleh Buku Komik.
Ada juga frekuensi 30 yang dicapai oleh Buku Pelajaran dan Buku Novel.
Modus dari data penjualan ini adalah jenis buku yang frekuensinya paling tinggi. Dalam hal ini, Buku Komik terjual paling banyak (40 eksemplar).
Jika ada dua atau lebih nilai data yang memiliki frekuensi tertinggi yang sama, maka data tersebut dikatakan memiliki modus ganda (bimodal, trimodal, dll.). Dalam kasus ini, frekuensi 30 muncul dua kali. Namun, frekuensi 40 lebih tinggi dari 30.
Jadi, modus dari data penjualan buku tersebut adalah Buku Komik karena memiliki frekuensi penjualan tertinggi (40 eksemplar).
(Catatan: Terkadang soal statistik bisa sedikit ambigu dalam definisi modus jika ada frekuensi yang sama. Namun, umumnya modus merujuk pada nilai dengan frekuensi tertinggi mutlak. Jika ada beberapa nilai dengan frekuensi tertinggi yang sama, maka semuanya dianggap modus.)
Soal 12: Menghitung Luas Jajar Genjang
Sebuah jajar genjang memiliki alas 20 cm dan tinggi 12 cm. Hitunglah luas jajar genjang tersebut.
Pembahasan:
Rumus luas jajar genjang sama dengan rumus luas persegi panjang:
Luas = alas × tinggi
Diketahui:
Alas = 20 cm
Tinggi = 12 cm
Luas = $20 text cm times 12 text cm$
Luas = $240 text cm^2$
Jadi, luas jajar genjang tersebut adalah $240 text cm^2$.
>
Penutup
Menguasai materi matematika kelas 7 semester 2 memang membutuhkan latihan yang konsisten. Contoh-contoh soal di atas mencakup berbagai topik penting yang sering diujikan. Dengan memahami konsep dasar dan melatih diri mengerjakan berbagai variasi soal, siswa diharapkan dapat meningkatkan kepercayaan diri dan meraih hasil belajar yang optimal.
Ingatlah bahwa matematika adalah sebuah proses. Jangan ragu untuk bertanya kepada guru atau teman jika ada materi yang belum dipahami. Teruslah berlatih, dan Anda akan semakin mahir dalam matematika!
>
